Research

Overview

Research in the Dynamics Lab is broadly focused on the modeling and analysis of systems of a dominantly mechanical character, specifically the dynamics of constrained rigid bodies and nonlinearly elastic rods. Our work spans the gamut from theoretical foundations to technological applications and utilizes analytical, computational, and experimental tools.

Selected Current Research

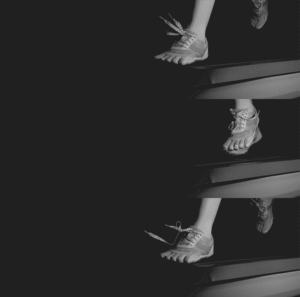
Shoelaces

Almost everyone has experienced the frustration of having shoelaces that just won’t stay tied. Interestingly, from a scientific point of view, little is known about the physical mechanisms that allow simple walking to untie a shoelace knot. We investigated the dynamics behind this everyday phenomena in our 2017 paper, “The Roles of Impact and Inertia in the Failure of a Shoelace Knot,” which appeared in the Proceedings of the Royal Society A. With the help of a high-speed video camera and a series of experiments, we showed that the failure can be attributed to the combined effects of repeated impact of the shoe with the ground and inertial effects caused by the motion of the shoelaces.

Our work on shoelaces received a great deal of media coverage, including an excellent piece by ABC 7’s Wayne Freedman.

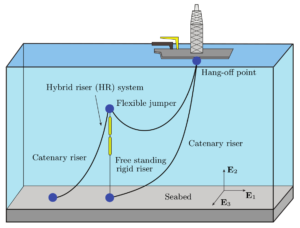
Mechanics of Marine Technologies

Many marine technologies have interesting nonlinear dynamics and fluid-structure interaction. The research we have conducted in this area includes oar blade design optimization and the modeling of an ocean wave energy converter (WEC) whose mass is modulated by the incident waves.

Our most recent research on this topic was focused on the dynamics of flexible risers. These massive structures are used to transport fluids to and from well heads on the ocean floor. Of particular interest was the mechanism by which these structures can become unstable.

Discrete Elastic Rods

Problems in rod mechanics are often difficult to solve numerically due to strong nonlinearities. By conceptually discretizing a rod into a series of masses, links, springs, and dampers, we are able to simulate a wide range of problems quickly and accurately. Recent research in this area has focused on the kinematics of discrete elastic rods and resulted in the publication of a book.

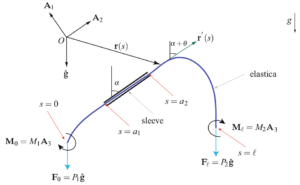
Fundamental Issues in Theories of Rods

While rod theories have been in existence since the time of Euler’s elegant work on the elastica in the 18th century, work on formulating more sophisticated rod theories continues to this day. Much of this work is driven by applications and features nonlinear theories. For example, recent research on rods with helical substructures and/or electrostatic effects have been motivated by the flurry of interesting experiments on DNA molecules. Another set of biology-inspired developments have arisen from the need to formulate models for growing plant stems and their time varying material properties.

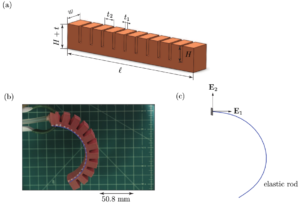
Mechanics of Soft Robots

Soft robots are a nascent technology which display great promise in a wide variety of applications. Their design, however, is most often based on trial-and-error. One factor that prevents roboticists from using a more systematic design procedure is the lack of practically useful, accurate models. Recent work in this area has focused on the development of constitutive laws for soft robot limbs.

Selected Previous Research

The biomechanics of the human spine has been a primary research area in recent years. The research has focused on the development of multiscale models for the human spine. These models range from models for the intervertebral joint to rod-based and multibody-based models for the spine. Supplemented by experimental work conducted in collaboration with Professor Jeffrey C. Lotz’s lab at UCSF, these models have been used to show the effects of total disc replacement on the mechanics of a vertebral joint and the stability of the spine in the sagittal plane. We have also developed a range of open-source models for the lumbar spine that are available on the Open-Sim platform. The collaboration with Jeff’s group has since evolved to examining cost-effective, portable methods to quantify orthopaedic biomechanics and physical therapies.

Further details on the research and publication can be found here. Collaborators on this research include the former students Jenni Buckley, Nur Adila Faruk Senan, Melodie Metzger, David Moody and Daniel Peters, and Professor Jeffrey Lotz.

Selected works on this topic include:

M. Christophy, M. Curtin, N. A. Faruk Senan, J. C. Lotz, and O. M. O’Reilly, On the Modeling of the Intervertebral Disc in Multibody Models for the Spine, Journal of Multibody System Dynamics, Online publication (2012).
M. Christophy, N. A. Faruk Senan, J. C. Lotz, and O. M. O’Reilly, A Muscloskeletal Model for the Lumbar Spine, Biomechanics and Modeling in Mechanobiology, Vol. 11, No. 1-2, 19-34 (2012).
J. C. Lotz, O. M. O’Reilly and D. M. Peters, Some Comments on the Absence of Buckling of the Ligamentous Human Spine in the Sagittal Plane, Mechanics Research Communications, Vol. 40, No. 1, 11-15 (2012).
O. M. O’Reilly, M. F. Metzger, J. M. Buckley, D. A. Moody and J. C. Lotz, On the Stiffness Matrix of the Intervertebral Joint: Application to Total Disc Replacement, ASME Journal of Biomechanical Engineering, Vol. 131, No. 8, 081007 (9 pages) (2009).

Dating back at least to Coriolis study of Billiards in the 1830s, toys and games have been the source of inspiration in dynamics for centuries. In the past three decades, several interesting toys have appeared. Among them, Euler’s disk, the Dynabee (Powerball), and Hoberman’s sphere. Working with former students Patch Kessler, David Gulick and Peter Varadi on these toys has lead to many surprising insights and conjectures. For Euler’s disk, the conjecture that the abrupt end to its motion is due to vibration driven loss of contact, that the spinup phenomenon in the Dynabee is related to a phenomenon known as resonance capture and features a rolling constraint, and that Hoberman’s sphere provides both a mechanical representation of Gauss’ mutation of space and a realization of Hamilton’s quaternions.

Further details on our work in this area can be found in an article by Mark Frauenfelder in Forefront.

Selected works on this topic include:

N. A. Faruk Senan and O. M. O’Reilly, On the Use of Quaternions and Euler-Rodrigues Symmetric Parameters with Moments and Moment Potentials, International Journal of Engineering Science, Vol. 47, No. 4, pp. 595-609 (2009).
D. W. Gulick and O. M. O’Reilly, On the Dynamics of the Dynabee, ASME Journal of Applied Mechanics, Vol. 67, No. 2, pp. 321-325 (2000).
P. Kessler and O. M. O’Reilly, The Ringing of Euler’s Disk, Regular and Chaotic Dynamics, Vol. 7, No. 1, pp. 49-60 (2002).
O. M. O’Reilly and P. C. Varadi, Hoberman’s Sphere, Euler Parameters and Lagrange’s Equations, Journal of Elasticity, Vol. 56, No. 2, pp. 171-180 (1999).

Brake squeal is a fugitive problem which has occupied researchers for decades. Although widely considered to be a friction-induced vibration phenomenon, the development of accurate models for braking systems and their array of components, and the challenges of analyzing and numerically integrating the resulting equations of motion has meant that this problem continues to feature in the vibrations and vehicle dynamics literature.

Our first research on this topic involved conducting a comprehensive review of work performed on disc brake squeal. This work lead to a publication in 2003 which has since been cited over 300 times and is the most cited work on brake squeal in the literature. Several open problems in the area also became apparent. The first of these was the lack of work on brake squeal induced by the braking event – most research assumed that the brake rotor’s speed was constant. Our resulting analysis with a simple model lead to the conclusions that two-dimensional stick-slip phenomena which naturally arose during a braking event could lead to a broad spectral excitation of the brake rotor. The second open problem was the issue of spectral analyses of linear M-C-K systems where the stiffness matrix was non-symmetric. Such systems feature prominently in models for braking systems. Using a pseudospectral analysis we were able to show how sensitive these models were to spectral instabilities near critical values of the system parameters. These results may eventually lead to an explanation for why brake squeal is so sensitive to the parameters of the braking system.

Collaborators on this research included the former students Patch Kessler, Nathan Kinkaid, and Anne-Lise Raphael, and Professors Panos Papadopoulos and Maciej Zworski.

Selected works on the aformentioned topic include:

N. M. Kinkaid, O. M. O’Reilly and P. Papadopoulos, Automotive Disc Brake Squeal, Journal of Sound and Vibration, Vol. 267, No. 1, pp. 105-166 (2003).
N. M. Kinkaid, O. M. O’Reilly, and P. Papadopoulos, On the Transient Dynamics of a Multi-Degree-of-Freedom Friction Oscillator: A New Mechanism for Disc Brake Noise, Journal of Sound and Vibration, Vol. 287, Issues 4-5, pp. 901-917 (2005).
P. Kessler, O. M. O’Reilly, A.-L. Raphael and M. Zworski, On Dissipation-Induced Destabilization and Brake Squeal: A Structured Pseudospectral Perspective, Journal of Sound and Vibration, Vol. 308, Number 1-2, pp. 1-11 (2007).

The research we conducted on this topic started in 2000 and was funded by a 4 year grant from the NSF and a one-year grant from the Center for Pure and Applied Mathematics at U.C. Berkeley.

Our two main former research projects on vehicle dynamics featured a motorcycle and Charles Taylor’s one-wheeled vehicle.

For the motorcycle, the research involved finding a robust algorithm for tracking motorcycles that is suitable for use in real time. Because of the engine-induced vibration in a motorcycle we found that using a set of 3 accelerometers and 3 gyroscopes was not as robust as expected. Instead, the algorithm we proposed and tested using a novel roll angle predictor which used motorcycle speed and a single gyrosope measurement of the angular velocity of the chassis along a vertical axis that corotated with the motorcycle. The experimental results of this research weren’t published, but the algorithm can be found in the paper cited below.

A former student in ME104, Tony Urry, brought Charles Taylor’s one-wheeled vehicle to our attention. A series of these machines was developed and patented by Taylor in the 1950s and 1960s. The goal of the research was to determine how this machine operated. Over the course of five years various models were developed and analyzed and eventually an understanding of how the machine stabilized was developed. Much work remains to be performed analyzing this machine, however the website we developed has lead to renewed interest in Taylor’s work. Hopefully, it will inspire others to reconstruct his prototypes.

Collaborators on this research included the former students Joshua Coaplen, Patch Kessler, Avery Jutkowitz, Eric Lew, Gwo-Jen Lo, Bayram Orazov, Dan Stevens, Peter Varadi, and Professors Karl Hedrick and Panos Papadopoulos.

Published works on this topic include:

J. P. Coaplen, P. Kessler, O. M. O’Reilly, D. M. Stevens and J. K. Hedrick, On Navigation Systems for Motorcycles: The Influence and Estimation of Roll Angle, Journal of Navigation, Vol. 58, No. 3, pp. 375-388 (2005).
E. S. Lew, B. Orazov and O. M. O’Reilly, The Dynamics of Charles Taylor’s Remarkable One-Wheeled Vehicle, Regular and Chaotic Dynamics, Vol. 13, No. 4, pp. 257-266 (2008).
P. C. Varadi, G.-J. Lo, O. M. O’Reilly and P. Papadopoulos, A Novel Approach to Vehicle Dynamics using the Theory of a Cosserat point and its Application to Collision Analyses of Platooning Vehicles, Vehicle System Dynamics, Vol. 32, No. 2, pp. 85-108 (1999).